Emergent order in bacterial collective motion
Active turbulence: Collective motion of swimming bacteria
Groups of self-propelled objects, represented by flocks of birds, schools of fish, and cell populations, are called "active matter", and are now being studied intensively as an interesting target of nonequilibrium statistical physics [A]. Among those examples, we are focusing on collective behavior of swimming bacteria. Swimming rod-shaped bacteria such as Eschelichia coli and Bacillus subtilis align to their neighboring bacteria due to their rod shapes [1]. This excluded volume interaction results in coherent collective motion at high density. In addition to the aligning excluded volume interaction, those bacteria also exhibit hydrodynamic interaction because they propel themselves by creating fluid flows by their flagella. As a result of this hydrodynamic interaction, the globally aligned state gets unstable and thus the bacterial orientations cannot align in the same direction over long distances. In the end, what we observe is a collective motion with a spatio-temporally fluctuating velocity field, in which bacterial orientations are aligned only locally but no global orientational order develops. This spaito-temporally chaotic collective motion is called bacterial turbulence or active turbulence [2].
Self-organization into vortex lattice orders
Can bacteria, which usually exhibit only chaotic collective motion, happen to show ordered motions? In the cases of collective motions of groups of living organisms or in vivo cell migrations, ordered and/or coordinated collective motion are often observed, and sometimes even required for their functions. Therefore, to address the questions of when and how such ordered motion emerges in bacterial collective motion, we investigate the coupling between bacterial collective motion and boundary conditions.
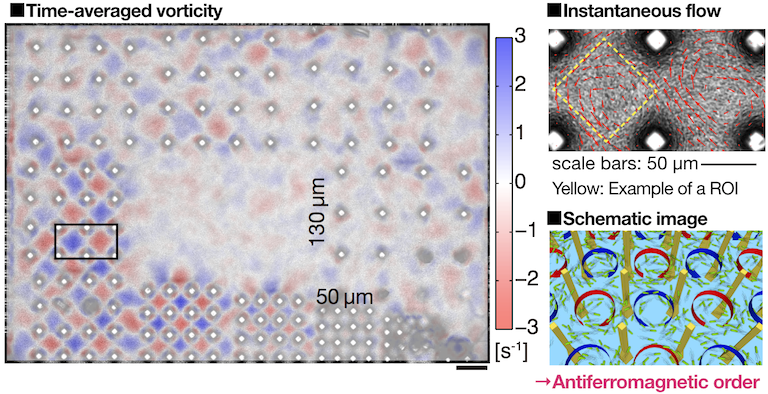
It has been understood that bulk bacterial turbulence far away from the boundaries can be described by hydrodynamic equations, which are obtained by adding an active force term to the Navier-Stokes equation. However, the boundary conditions for those active hydrodynamic equations are not as simple as those for the Navier-Stokes equation, and thus there was a need of experimental inputs on the behavior of bacterial turbulence in the presence of boundaries. In this spirit, we constructed microscopic pillar arrays with an advanced photolithography technique and let bacterial turbulence flow into those structures to observe its behavior. We arranged pillars with a diameter of 20 µm and a height of 150 µm in square lattices, with their lattice constants ranging from 50 µm to 130 µm, and the behavior of bacterial turbulence was observed simultanelously (Fig. 1). As a result, we found that, in the lattice with the lattice constant of 70 µm, bacteria self-organize in antiferromagnetic vortex lattice order, in which they form counter-rotating vortices between pillars [2]. Finite size effects were quantitatively assessed by changing the vortex lattice size from 3×3 to 8×8, which confirmed that the system has both spatially and temporally stable long-range vortex order, which spans the whole lattice even in the infinitely large system size limit. Our results imply that the constraints as weak as only 4% of volume fractions can trigger the emergence of long-range order from chaotic bacterial collective motion.
Recently, we have also succeeded in understanding the principle of this vortex order formation in terms of real space topology [3]. Specifically, we have found that microscopic pillars can behave as topological defects of the flow field of bacterial turbulence. Such a property has been observed not only within the pillar arrays but also for an isolated single pillar. This led us to unravel novel boundary conditions for bacterial turbulence, with which the hydrodynamic equations reproduce the topological property of the pillars as well as macroscopic vortex lattice formations. By integrating our findings, we have constructed a general framework to extract various vortex order from microbial populations.
References
(Takeuchi Lab)
[1] D. Nishiguchi, K. H. Nagai, H. Chaté and M. Sano, Phys. Rev. E 95, 020601(R) (2017) [pdf, web].
[2] D. Nishiguchi, I. S. Aranson, A. Snezhko and A. Sokolov, Nat. Comm. 9, 4486 (2018) [web].
[3] H. Reinken, D. Nishiguchi, S. Heidenreich, A. Sokolov, M. Bär, S. H. L. Klapp and I. S. Aranson, Comm. Phys. in press (2020).
(other groups)
[A] A review on recet experiments and theories: M. Bär, R. Großmann, S. Heidenreich and F. Peruani, Annu. Rev. Cond. Matt. Phys. 11, 441 (2019) [web]; M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys. 85, 1143 (2013) [web].
Main contributors
D. Nishiguchi
