KPZ universality in growing interfaces of liquid-crystal turbulence
Growing interfaces of liquid-crystal turbulence and KPZ
Physics of critical phenomena at equilibrium has been established on the basis of various experiments, exact solutions and other approaches, which led to the invention of fundamental frameworks such as the renormalization group theory and the conformal field theory. One may ask then: does a similarly profound physics exist for systems driven out of equilibrium? No one knows the answer yet, but recent theoretical developments on the Kardar-Parisi-Zhang (KPZ) universality class, the fundamental class describing random growth processes [A], have established an example in which various statistical properties can be derived exactly, despite being far from equilibrium [1,B].
We are studying this problem experimentally, focusing on growing interfaces of turbulent domains in electrically driven liquid crystal convection. This turbulent state called DSM2 consists of densely entangled topological defects, and can be generated by shooting ultraviolet laser pulses under a sufficiently high voltage applied to the system. By changing the beam shape of the laser, we can generate both circular and flat interfaces (Movies 1 and 2).
Universal interface fluctuations indicate a subclass structure of KPZ

Measuring statistical properties of interface fluctuations, we obtain the same set of the KPZ scaling exponents for both cases, but nevertheless, fluctuations of the circular and flat interfaces are found to exhibit distinct distribution and correlation functions. The obtained functions agree with the results previously derived for solvable models of the KPZ class [1,B]; in particular, the distribution function for the circular and flat interfaces is shown to be the largest-eigenvalue distribution for GUE and GOE random matrices, respectively, called the Tracy-Widom distribution in random matrix theory (see Fig. 1). This result implies that universality arises even in detailed statistical properties such as the distribution and correlation functions. Moreover, the KPZ class actually splits into a few universality "subclasses" according to the global geometry of interfaces (or the initial condition), characterized by different distribution and correlation functions: here we identified the circular (or curved) and flat subclasses [2,3].
Analytical developments on the KPZ class are remarkable, yet there do exist important statistical properties that remain unsolved, such as the time correlation. We are determining such unsolved properties experimentally, by means of careful analysis of the growing liquid-crystal turbulence. In particular, on the time correlation, we found even qualitative differences between the circular and flat interfaces, regarding symmetry between positive and negative fluctuations and persistence of correlation [3]. For the circular interfaces, we showed that correlation persists forever in time. This anomalous result was subsequently confirmed by theory [4], and eventually a mathematical theorem was established [C].
Designing the initial condition arbitrarily by laser holographic technique
The KPZ universal fluctuations are classified into universality subclasses, which are determined mainly by the initial condition. This led us to extend our experimental system so that the initial condition can be designed arbitrarily, which we realized by adapting a laser holographic technique (Movie 3) [5].
This new system allows us to study KPZ universal fluctuations for various geometries, which were hitherto inaccessible. For example, from a ring of a finite radius, we have a pair of interfaces growing outward and inward from the initial ring. We found, both experimentally and numerically, that the outgrowing interfaces show crossover from the flat subclass to the circular subclass, and that the ingrowing interfaces behave like flat interfaces, until they eventually deviate from the KPZ class and collapse near the center of the ring [5].
Theoretically, a variational formula was proposed as a useful tool to deal with KPZ fluctuations for general initial conditions [D], which has indeed been used for many analytical studies. We proposed a method to evaluate the variational formula numerically, and showed that it can be used to reproduce our experimental and numerical results quantitatively [5]. This underlines the practical importance of the variational formula, which can predict and account for fluctuation properties of interfaces for general initial conditions.
Towards the detection of the stationary KPZ subclass
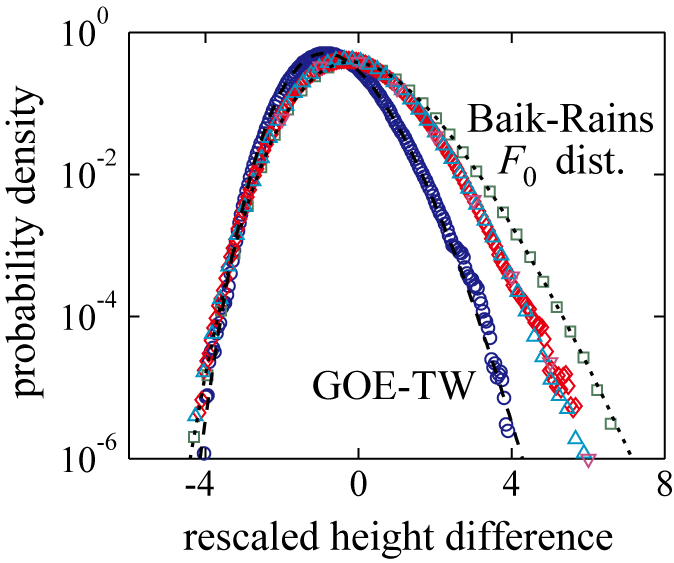
It is theoretically known that the circular and flat subclasses are not the only ones that exist: indeed, the stationary subclass, which describes the stationary state of the KPZ-class interfaces, is also well established [1,B]. This subclass is however practically inaccessible in experiments, because it takes infinitely long time to reach it. To circumvent this difficulty, we studied, instead of the height $h(x,t)$, the height difference between two times,
$\Delta h(x,\Delta t, t_0) = h(x, t_0+\Delta t) - h(x, t_0)$.
Thereby we found crossover between the flat and stationary subclasses, first numerically at high precision (Fig. 2), then we identified indications of the same crossover in the experiment [6].
KPZ half-space problem
If an interface ends at a boundary, the boundary condition is expected to affect the fluctuation properties. This is well studied by the name of the KPZ half-space problem, which deals with interfaces growing in a semi-infinite region $x \geq 0$ with a given boundary condition at $x=0$, and several universality subclasses have been established. In particular, when a circular interface grows with its slope at $x=0$ fixed at a large positive value, the GSE Tracy-Widom distribution from random matrix theory is predicted. However, experimentally, it is in general difficult to impose a well-defined boundary condition for growing interfaces. Experiments on the KPZ half-space problem seem to be therefore a mission impossible.
To overcome this difficulty, we propose the "biregional" interface growth problem, in which the interface grows at different speeds in the left and right regions [7] (Movie 4). Although experimental tests of the GSE Tracy-Widom distribution are on the way, we showed numerically that our biregional setting indeed results in the universal distributions predicted for the KPZ half-space problem [7]. The biregional interface growth is therefore a useful approach to study the KPZ half-space problem experimentally and numerically.
References
(Takeuchi Lab)
[1] For an introductory review on modern aspects of KPZ: K. A. Takeuchi, Physica A 504, 77 (2018) [web, preprint].
[2] K. A. Takeuchi and M. Sano, Phys. Rev. Lett. 104, 230601 (2010) [pdf, web]; K. A. Takeuchi, M. Sano, T. Sasamoto, and H. Spohn, Sci. Rep. 1, 34 (2011) [pdf, web].
[3] K. A. Takeuchi and M. Sano, J. Stat. Phys. 147, 853 (2012) [web, preprint].
[4] J. De Nardis, P. Le Doussal, and K. A. Takeuchi, Phys. Rev. Lett. 118, 125701 (2017) [pdf, web].
[5] Y. T. Fukai and K. A. Takeuchi, Phys. Rev. Lett. 119, 030602 (2017) [pdf, web]; Phys. Rev. Lett. 124, 060601 (2020) [pdf, web].
[6] K. A. Takeuchi, Phys. Rev. Lett. 110, 210604 (2013) [pdf, web].
[7] Y. Ito and K. A. Takeuchi, Phys. Rev. E 97, 040103(R) (2018) [pdf, web].
(other groups)
[A] A.-L. Barabási and H. E. Stanley, Fractal Concepts in Surface Growth (Cambridge Univ. Press, Cambridge, 1995).
[B] Other reviews on exact studies on KPZ: T. Kriecherbauer and J. Krug, J. Phys. A 43, 403001 (2010) [web]; I. Corwin, Random Matrices Theory Appl. 1, 1130001 (2012) [web]; H. Spohn, Lecture Notes of the Les Houches Summer School, 104, 177-227 (2017) [web, preprint].
[C] K. Johansson, Probab. Theory Relat. Fields 175, 849 (2019) [web].
[D] J. Quastel and D. Remenik, Springer Proceedings in Mathematics & Statistics, 69, 121 (2014) [web, preprint].
Main contributors
K. A. Takeuchi, Y. T. Fukai, Y. Ito, T. Iwatsuka
