液晶の位相欠陥乱流における普遍的な非平衡臨界現象の発見
吸収状態への相転移と directed percolation (DP) 普遍クラス
吸収状態、すなわち、一度入ったら二度と出られない状態への相転移は、伝染病、森林火災の拡がりから、触媒反応や細胞のシグナル伝達に至るまで、様々な場面で現れます。このような吸収状態転移は非平衡固有の相転移現象として熱心に研究されており、多種多様の数値モデルが転移点において Directed Percolation (DP) クラスと総称される普遍的な臨界現象を示すことが数値的・理論的に確立していますが、実験的にそれが十分な信頼性をもって観測されたことはなく、大きな未解決問題として認識されていました[A,1]。
DPクラス相転移の発見
我々は液晶電気対流の乱流間相転移において臨界現象の精密な実験を行い、DPクラスに属する相転移の初の実験的証拠を得ることに成功しました[1-3]。ある種のネマチック液晶は電圧を印加すると対流が起こり、電圧が高いと乱流状態が実現します。この乱流にはdisclinationと呼ばれる位相欠陥が大量に発生した状態(DSM2)とそれが皆無な状態(DSM1)の二種類が存在し、転移点近傍ではDSM1の中をDSM2のパッチが動き回る、時空間欠性と呼ばれる状態が実現します(ムービー1)。電圧を下げ、転移点に到達するとDSM2は消えてしまいますが、位相欠陥からなるDSM2はほとんど自発生成しないため、DSM2が全滅した状態はほぼ完全な吸収状態であり、従ってDSM1-DSM2転移は吸収状態転移の一例になっています。
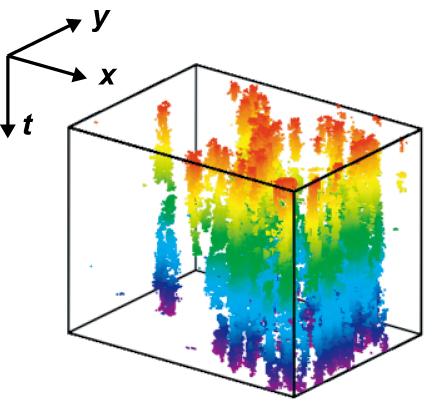
転移点近傍の時空間ダイナミクスを見てみると(図1)、パッチ状のDSM2が時間軸方向に浸透を起こしているとみなすこともでき、もともとは異方的浸透現象のクラスであったDP転移として、期待される性質を備えていることがわかります。そこで我々はDSM1-DSM2転移の臨界現象の静的・動的側面を特徴づける精密な実験を行い、総計12個の臨界指数、5個の普遍スケーリング関数を直接測定することに成功しました(図2)[1-3]。それらは全て空間2次元のDPクラスのものと良い精度で一致し、本実験がDPクラスの普遍的な臨界現象を示していることが明らかとなりました。これにより、世界で初めてDP転移の実験証拠が発見されたこととなり、実験の欠如という分野積年の課題が解決されました[B]。
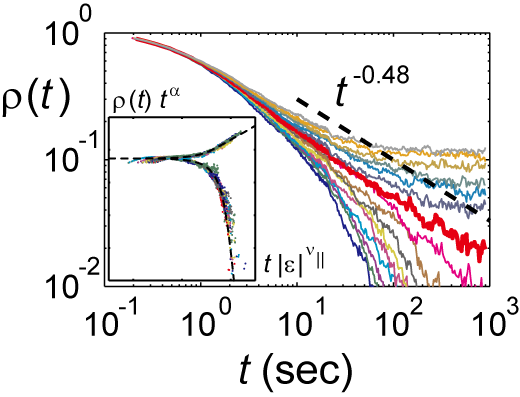
図2: 印加電圧を急降下させた場合のDSM2面積(オーダーパラメータ)$\rho(t)$の時間変化。ターゲット電圧が転移点の場合(赤線)は冪的に$\rho(t) \sim t^{-\alpha}$のように減衰し、その指数 $\alpha=0.48 \pm 0.05$ は(2+1)次元DPの臨界指数 $\alpha = 0.45$ と一致しています。横軸縦軸を適切にリスケールすると全ての曲線が重なり、数値的に求めたDP普遍スケーリング関数に一致します(挿図)。[2,3]
本研究により自然界に実在することが判明したDP転移は、その後、他グループの研究によって、水などの単純流体にせん断をかけたときの層流乱流転移でも現れることがわかりました[C]。また、我々は、理論家との共同研究により、冷却原子気体などの量子流体における乱流転移でもDPが現れる可能性を数値計算で示しました[4]。このように、実験や現実的なモデルに基づいて、非平衡現象と吸収状態転移、DPクラスとの関係が調べられるようになってきたのが最近の展開であり、当研究室でも関心を持ち続けています。
吸収状態転移が示す特徴的なヒステリシス
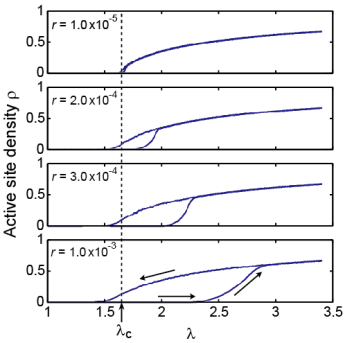
臨界現象を支配するスケーリング則を理解することで、DSM1-DSM2転移に関する過去の実験事実を説明することもできます。例えば、DSM1-DSM2転移は印加電圧をスイープするとヒステリシスを示し(ムービー2)、その幅 $\Delta V$ はスイープ速度 $r$ に対して $\Delta V \sim r^\kappa$ ($\kappa = 0.5$-$0.6$) のように冪的に依存することが知られています[D]。我々はこのヒステリシスをDSM2の極めて稀な自発生成によるものと考え、DPダイナミクスに稀な自発生成を付加したモデルを導入しました。このモデルはヒステリシスを定性的に再現するだけでなく(ムービー3)、ヒステリシスの幅に関する指数 $\kappa$ も実験と一致しました(図3)[5]。理論的にも、指数 $\kappa$ は吸収状態転移のオーダーパラメータ臨界指数 $\beta'$ と $\kappa = 1/(\beta'+1)$ という簡潔なスケーリング関係式で結ばれることが示せます[5]。これは、液晶系に限らず、一般に測定可能な量が限られがちな実験系において、ヒステリシスの計測から臨界指数を推定できる、有用な手段になりうると期待しています。
参考文献
(当研究室)
[1] 竹内一将, 日本物理学会誌 70, 599 (2015) (2015年8月号解説記事)[web].
[2] K. A. Takeuchi, M. Kuroda, H. Chaté, and M. Sano, Phys. Rev. Lett. 99, 234503 (2007) [pdf, web].
[3] K. A. Takeuchi, M. Kuroda, H. Chaté, and M. Sano, Phys. Rev. E 80, 051116 (2009) [pdf, web].
[4] M. Takahashi, M. Kobayashi, and K. A. Takeuchi, arXiv:1609.01561 [web].
[5] K. A. Takeuchi, Phys. Rev. E 77, 030103(R) (2008) [pdf, web].
(他グループ)
[A] H. Hinrichsen, Adv. Phys. 49, 815 (2000) [web]; M. Henkel, H. Hinrichsen, and S. Lübeck, Non-Equilibrium Phase Transitions, Volume I: Absorbing Phase Transitions (Springer, Dordrecht, 2008).
[B] H. Hinrichsen, Physics 2, 96 (2009) [web].
[C] M. Sano and K. Tamai, Nat. Phys. 12, 249 (2016) [web]; G. Lemoult et al., Nat. Phys. 12, 254 (2016) [web].
[D] S. Kai, W. Zimmermann, M. Andoh, and N. Chizumi, Phys. Rev. Lett. 64, 1111 (1990) [web].
主に関わっているメンバー
竹内 一将
