液晶トポロジカル欠陥の3次元ダイナミクス観察
液晶のトポロジカル欠陥とは?

液晶のうち、ネマティック液晶と呼ばれる種類のものは、棒状分子が向きを揃える配向秩序を示しますが、向きを揃えられない特異点を生じることがあり、トポロジカル欠陥と呼ばれます。図1は、そのうち最も基本的な種類であるdisclinationと呼ばれる欠陥の模式図です。2次元ではdisclinationは点欠陥で、欠陥の周りで向きが何回転したかをあらわす「巻き数」というトポロジカル数で区別・分類されます。欠陥には相互作用が働き、巻き数$\pm 1/2$の点欠陥は引き合ってぶつかり、消えてしまう、対消滅という現象がみられます。3次元ではdisclinationは線欠陥となり(図1)、再結合と呼ばれる線欠陥の繋ぎ換えなど、トポロジカル欠陥に特徴的な現象を示しますが、そのダイナミクスを3次元空間で捉えることは困難でした。
液晶トポロジカル欠陥の3次元ダイナミクス観察
液晶トポロジカル欠陥の3次元ダイナミクスを観察するため、我々は蛍光分子が欠陥に集積する性質[A]を利用して欠陥を可視化し、高速の共焦点顕微鏡で3次元画像を撮影しました。液晶に電圧をかけて乱流を起こし、欠陥を大量に生成しておいてから、印可電圧を除去して欠陥の緩和過程を引き起こします。すると、大量の線欠陥が現れて、再結合やループ収縮などを起こしながら縮んでいき、消滅する過程が捉えられました[1]。ムービー1は、その際に見られた再結合の様子です。
欠陥再結合のスケーリング則と「自発的対称性の回復」
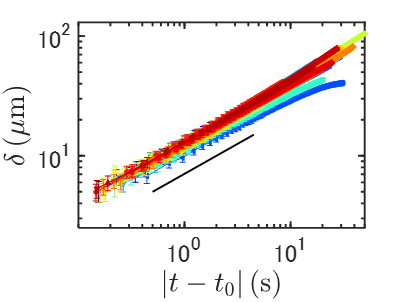
我々は、液晶中のトポロジカル線欠陥の再結合について詳しく解析を行いました[1]。欠陥同士の最短距離 $\delta(t)$ が再結合時刻 $t_0$ に向けてどのように変化するかを調べると、\[\delta(t) \sim |t-t_0|^{1/2}\]というスケーリング則が成り立つことが明らかになりました(図2)。これは2次元点欠陥ではよく知られた関係で、3次元液晶でも直線的な線欠陥に対しては最近理論的に予言されました[B]が、3次元的な実験で検証されたのは初めてであり、曲がった欠陥同士でも成り立つことがわかりました。興味深いことに、同じスケーリング則は超流動の量子渦糸の再結合でも現れることが知られており[C]、異なる系でもトポロジカル欠陥が共通の性質をもちうることを示唆しています。

また、2次元液晶では、2つの点欠陥が近づいて対消滅する際、流れ場の効果によって2つの欠陥は非対称に運動することが知られています[D]。では、3次元液晶の再結合では、そのような非対称性は存在するでしょうか。素朴には、図1に示すように、次元が違っても欠陥周りで配向が回転していることに違いはなく、2次元と同様の非対称性が3次元でも現れてよいように思われます。しかし我々は、周囲の欠陥等の影響を取り除く解析を行ったところ、意外なことに3次元では非対称性が消失し、再結合が対称に起こることを見出しました。我々は、欠陥に関するトポロジーとエネルギーの観点から、図3のような「自発的対称性の回復」とも言えるメカニズムで、非対称性の消失を説明しました[1]。
このような液晶中の欠陥ダイナミクスについての理解は、液晶の緩和過程や乱流状態など、非平衡状態の理解に重要な手がかりを与えてくれます。液晶だけではありません。トポロジカル線欠陥が、超流動液体における量子渦糸や宇宙論における宇宙ひもなど、扱う対象も時空スケールも大きく異なる他の物理系でも見られることから、制御性が高く光学観察に適した液晶実験で得られた知見は、物理の広い分野に貢献する可能性を秘めているのです。
参考文献
(当研究室)
[1] Y. Zushi and K. A. Takeuchi, Proc. Natl. Acad. Sci. USA 119, e2207349119 (2022) [web]; プレスリリース 「液晶中に生じるトポロジカルな「ひも」の3次元的な動きを捉えることに成功」[link].
(他グループ)
[A] T. Ohzono, K. Katoh, and J. Fukuda, Sci. Rep. 6, 36477 (2016) [web].
[B] C. Long, X. Tang, R. L. B. Selinger, and J. B. Selinger, Soft Matter 17, 2265-2278 (2021) [web]; C. D. Schimming and J. Viñals, Soft Matter 18, 2234-2244 (2022) [web].
[C] G. P. Bewley et al., Proc. Natl. Acad. Sci. USA 105, 13707-13710 (2008) [web]; E. Fonda et al., Proc. Natl. Acad. Sci. USA 111, 4707-4710 (2014) [web].
[D] G. Tóth, C. Denniston, and J. M. Yeomans, Phys. Rev. Lett. 88 105504 (2002) [web];
D. Svenšek and S. Žumer, Phys.Rev. E 66, 032712 (2002) [web].
主に関わっているメンバー
図司 陽平、竹内 一将
