時系列解析による大自由度力学系の不安定性計測
カオス
カオスは、初期条件のわずかな違いが短時間で指数関数的に大きくなる現象です。 中でも大自由度のカオスは、気象などの流体現象をはじめ、様々な自然現象で見られますし、電気化学反応などのモデル実験系もあります。心室細動もカオスとの関係が議論されてきました。 大自由度カオス実験系の理解は、こうした非平衡の物理現象を理解する一つの鍵になります。
Lyapunov指数
カオスは、軌道に与えた摂動の指数関数的な成長率で特徴づけられています。 この成長率のことをLyapunov指数 [1] と呼びます。 Lyapunov指数は、系の不安定性の指標となるだけでなく、アトラクター次元や力学系的エントロピーと直接結ばれ、 大自由度カオスの示量性の定義にも使われる重要な量です。 また、不安定性は、気象予報のため重要なデータ同化、心室細動の除去法としても研究提案のあるカオス制御など、応用面でも重要な役割を果たします。
大自由度系でのLyapunov指数測定の問題
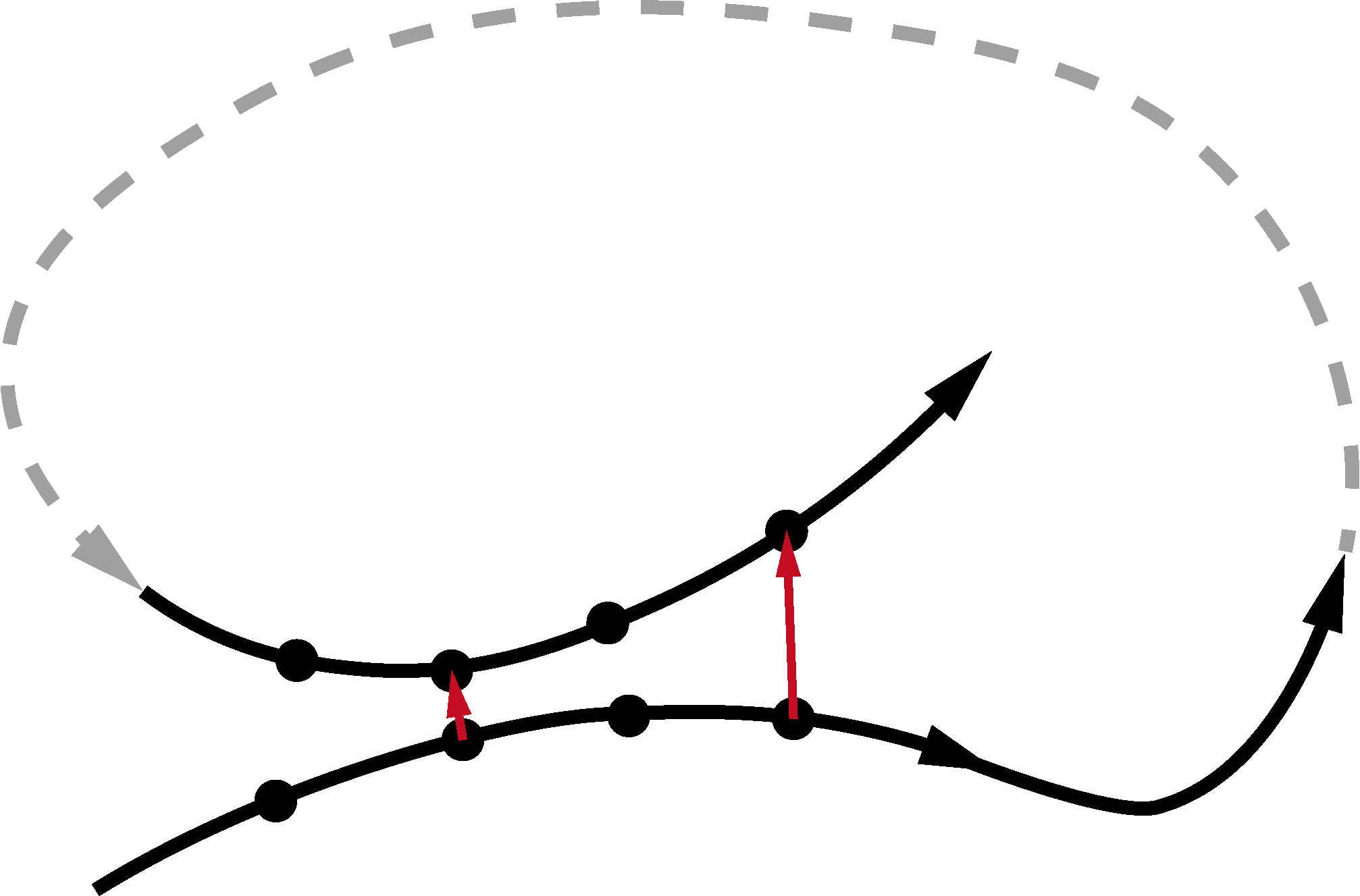
実験的にLyapunov指数を測定する最も標準的な方法は、 時系列データを空間上にプロットすることで得られる一つの軌跡のうち、 それが再帰することで、互いに近傍になる二点を摂動とみなし、その指数関数的な成長率を測定する方法です。 ところが、大自由度実験系の場合、再帰イベントの頻度が自由度に対して著しく減少するため、 現実的な時間でLyapunov指数を測定することができません。 近年は、機械学習を用いて、時系列データから大自由度カオスのLyapunov指数を測定する手法が提唱されました [A]。 しかし、この手法の適用には様々なパラメータを注意深く調整する必要があり、数値計算の答え合わせができない実験データに対する実用性は未知数です。また論文で示された検証は全自由度の時系列データを使っているなど、必ずしも大自由度系のLyapunov指数測定の難しさが解決したとは言えません。
対称性の高い大自由度系でLyapunov指数を測定する新手法を提案
我々は、大自由度カオスのうち、対称性の高い系、つまり局所的なダイナミクスが少数の力学変数で記述される系に着目しました。 例えば、大域結合系では、局所的なダイナミクスが局所的な力学変数と平均場の2変数で記述されます。 この対称性に着目することで、再帰イベントに関わる自由度を実効的に著しく落とし、 Lyapunov指数を測定するのに十分な数の再帰イベントを得ることが可能となります。
我々は、このアイディアを二つの大域結合系、 大域結合ロジスティック写像と大域結合リミットサイクル振動子に適用し、 数値的に検証しました。 その結果、時系列データから推定したLyapunov指数は、 標準的な数値計算方法で得られた真の値を再現しました。 この知見を活かし、大域結合系以外の大自由度系カオスに対しても同様のアイディアを適用できないか、研究を進めています。
参考文献
(当研究室)
[1] T. P. Shimizu and K. A. Takeuchi, Chaos 28, 121103 (2018) [pdf, web].
(他グループ)
[A] J. Pathak, Z. Lu, B. R. Hunt, M. Girvan, and E. Ott, Chaos 27, 121102 (2017) [web].
主に関わっているメンバー
清水 太朗
